Contains basic algorithms to manipulate images. More...

#include <Algorithms.h>

Static Public Member Functions
static int	doubleEqual (double a, double b)
	The resulting rounding error after floating point computations depend on the specific operations done.The same number computed by different algorithms could present different rounding errors.For a useful comparison, an estimation of the relative rounding error should be considered and compared to a factor times EPS.The factor should be related to the cumulated rounding error in the chain of computation.Here, as a simplification, a fixed factor is used. More...

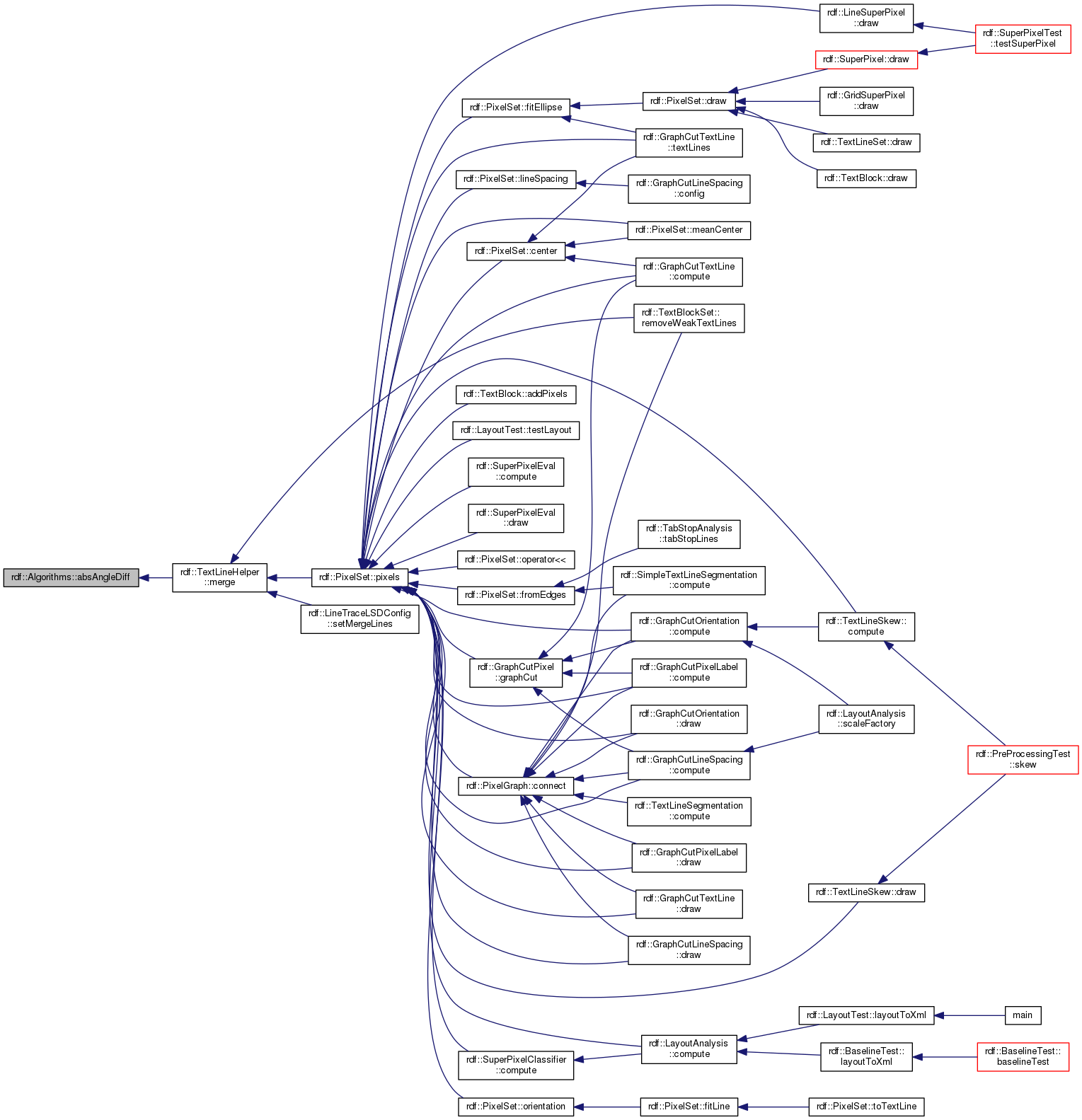
static double	absAngleDiff (double a, double b)

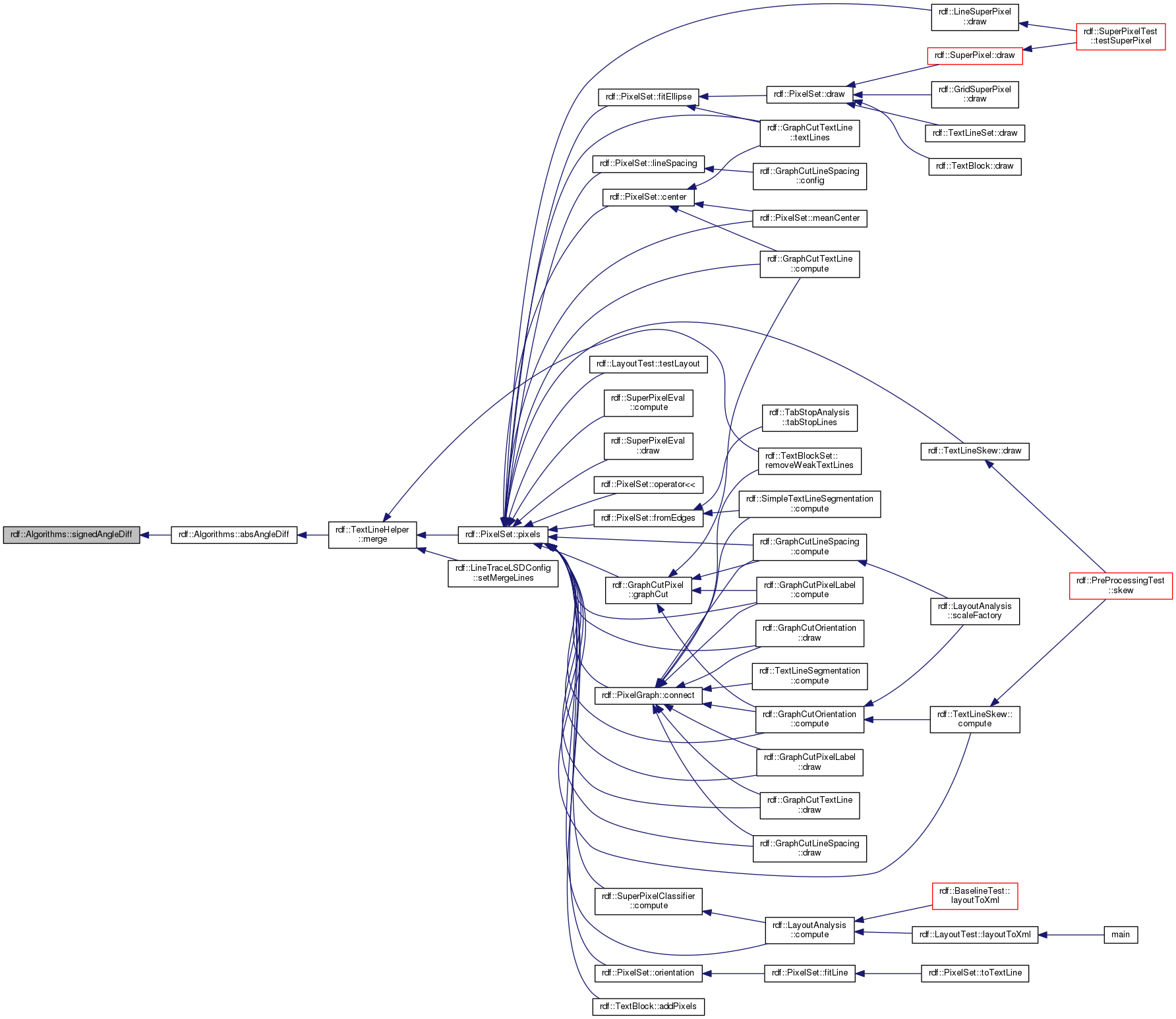
static double	signedAngleDiff (double a, double b)

static double	min (const QVector< double > &vec)
	Returns the minimum of the vector or DBL_MAX if vec is empty. More...

static double	max (const QVector< double > &vec)
	Returns the maximum value of vec or -DBL_MAX if vec is empty. More...

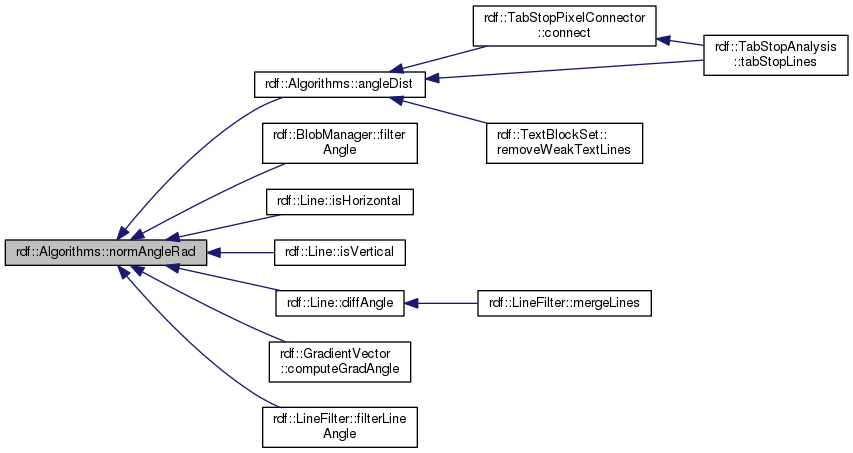
static double	normAngleRad (double angle, double startIvl=0.0, double endIvl=2.0 *CV_PI)
	Computes the normalized angle within startIvl and endIvl. More...

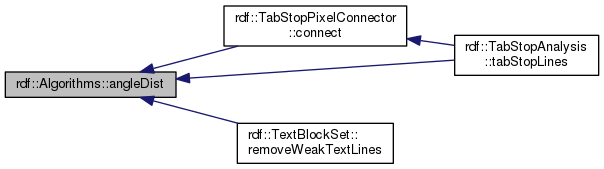
static double	angleDist (double angle1, double angle2, double maxAngle=2.0 *CV_PI)
	Computes the distance between two angles. Hence, min(angleDiff, CV_PI*2-(angleDiff)) More...

template<typename numFmt >
static double	statMoment (const QList< numFmt > &valuesIn, double momentValue, bool interpolated=true)
	Computes robust statistical moments (quantiles). More...

Detailed Description

Contains basic algorithms to manipulate images.

Member Function Documentation

double rdf::Algorithms::absAngleDiff	(	double	a,
		double	b
	)

static

Here is the caller graph for this function:

double rdf::Algorithms::angleDist	(	double	angle1,
		double	angle2,
		double	maxAngle = `2.0*CV_PI`
	)

static

Computes the distance between two angles. Hence, min(angleDiff, CV_PI*2-(angleDiff))

Parameters

angle1	The angle1.
angle2	The angle2.

Returns: The angular distance.

Here is the caller graph for this function:

int rdf::Algorithms::doubleEqual	(	double	a,
		double	b
	)

static

The resulting rounding error after floating point computations depend on the specific operations done.The same number computed by different algorithms could present different rounding errors.For a useful comparison, an estimation of the relative rounding error should be considered and compared to a factor times EPS.The factor should be related to the cumulated rounding error in the chain of computation.Here, as a simplification, a fixed factor is used.

Parameters

a	Input a
b	Input b

Returns: equal if relative error <= factor x eps

double rdf::Algorithms::max ( const QVector< double > & vec )

static

Returns the maximum value of vec or -DBL_MAX if vec is empty.

Parameters

vec	A vector with double values.

Returns: the maximum

double rdf::Algorithms::min ( const QVector< double > & vec )

static

Returns the minimum of the vector or DBL_MAX if vec is empty.

Parameters

vec	A vector with double values.

Returns: the minimum

Here is the caller graph for this function:

double rdf::Algorithms::normAngleRad	(	double	angle,
		double	startIvl = `0.0`,
		double	endIvl = `2.0*CV_PI`
	)

static

Computes the normalized angle within startIvl and endIvl.

Parameters

angle	The angle in rad.
startIvl	The intervals lower bound.
endIvl	The intervals upper bound.

Returns: The angle within [startIvl endIvl].

Here is the caller graph for this function:

double rdf::Algorithms::signedAngleDiff	(	double	a,
		double	b
	)

static

Here is the caller graph for this function:

template<typename numFmt >

static double rdf::Algorithms::statMoment	(	const QList< numFmt > &	valuesIn,
		double	momentValue,
		bool	interpolated = `true`
	)

inlinestatic

Computes robust statistical moments (quantiles).

Parameters

valuesIn	The statistical set (samples).
momentValue	The statistical moment value (0.5 = median, 0.25 and 0.75 = quartiles).
interpolated	A flag if the value should be interpolated if the length of the list is even.

Returns: The statistical moment.

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

src/Core/Algorithms.h
src/Core/Algorithms.cpp

Static Public Member Functions

Detailed Description

Member Function Documentation